Первісна (понеділок)

Первісна

Для знаходження функції за її похідною застосовують операцію інтегрування, обернену до операції диференціювання.

Якщо для всіх x$x$ із заданого проміжку [a;b]$[a;b]$

F′(x)=f(x),$$F^{\prime }(x)=f(x),$$

то F(x)$F(x)$ називається первісною для f(x)$f(x)$ на цьому проміжку.

Загальний вигляд первісних для функції f(x)$f(x)$ на проміжку [a;b]$[a;b]$ є F(x)+C$F(x)+C$, де C$C$ — довільна стала, а F(x)$F(x)$ — одна з первісних для f(x)$f(x)$ на проміжку [a;b]$[a;b]$.

Правила знаходження первісних

1. Якщо F(x)$F(x)$ — первісна для f(x)$f(x)$, а G(x)$G(x)$ — первісна для g(x)$g(x)$, то F(x)+G(x)$F(x)+G(x)$ — первісна для f(x)+g(x)$f(x)+g(x)$.
2. Якщо F(x)$F(x)$ — первісна для f(x)$f(x)$, а k$k$ — стала, то k⋅F(x)$k\cdot F(x)$ — первісна для k⋅f(x)$k\cdot f(x)$.
3. Якщо F(x)$F(x)$ — первісна для f(x)$f(x)$, а k (k≠0)$k(k\ne 0)$ і b$b$ — сталі, то 1k⋅F(kx+b)$\frac{1}{k}\cdot F(kx+b)$ — первісна для f(kx+b)$f(kx+b)$.

Площа криволінійної трапеції

Нехай на відрізку [a;b]$[a;b]$ осі Ox$Ox$ задано неперервну функцію f(x)$f(x)$, яка не змінює на ньому знак. Фігуру, обмежену графіком цієї функції, відрізком [a;b]$[a;b]$, прямими x=a$x=a$ і x=b$x=b$ (рис. 1), називають криволінійною трапецією.

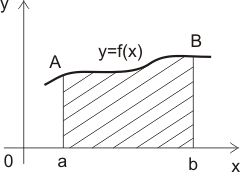
Рис.1. Площа криволінійної трапеції.

Площа криволінійної трапеції aABb$aABb$ (рис. 1), обмежена віссю Ox$Ox$, прямими x=a$x=a$ і x=b$x=b$ та графіком невід’ємної функції y=f(x)$y=f(x)$ на відрізку [a;b]$[a;b]$, визначається за формулою

S=∫baf(x)dx.$$S={\int }_a^{b}f(x)dx.$$

Якщо функція f(x)$f(x)$ неперервна і невід’ємна на відрізку [a;b]$[a;b]$ і F(x)$F(x)$ — первісна для f(x)$f(x)$ на відрізку [a;b]$[a;b]$, то площу S$S$ криволінійної трапеції знаходять за формулою Ньютона-Лейбніца:

S=∫baf(x)dx=F(b)−F(a).$$S={\int }_a^{b}f(x)dx=F(b)-F(a).$$

Коли неперервна функція f(x)≤0$f(x)\le 0$ на [a;b]$[a;b]$, то обчислити площу відповідної криволінійної трапеції можна за формулою:

S=−∫baf(x)dx=∫abf(x)dx.$$S=-{\int }_a^{b}f(x)dx={\int }_b^{a}f(x)dx.$$

Якщо фігура обмежена графіками двох неперервних функцій f1(x)$f_1(x)$ та f2(x)$f_2(x)$ і двома прямими x=a$x=a$ і x=b$x=b$, де f1(x)≥f2(x)$f_1(x)\ge f_2(x)$ на відрізку [a;b]$[a;b]$, то площу такої фігури шукають за формулою:

S=∫baf1(x)dx−∫baf2(x)dx=$$S={\int }_a^b{f}_1(x)dx-{\int }_a^b{f}_2(x)dx=$$

=∫ba(f1(x)−f2(x))dx.

Завдання обчислення інтегралів

Тести інтеграли