Поняття множини (четвер)

Поняття множини.

Дії над множинами

      Тему «Множина» ми вже розглядали у курсі «Інформатика 10 клас», тому цей урок буде оглядовим. Нагадаємо основні означення теорії множин.

      Поняття множини належить до первісних, воно не означається. Множина - це сукупність, зібрання деяких предметів будь-якої природи, наприклад: множина учнів класу, множина цифр десяткової нумерації, множина букв українського алфавіту, множина міст держави, множина будинків на ву­лиці тощо.

      Для позначення множин використовуються про­писні літери латинського алфавіту або фігурні дуж­ки: множина А або {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

      Озн 1. Предмети, з яких складається мно­жина, називаються її елементами.

      Наприклад, а = 5 - елемент множини цифр десяткової нумерації;

                             Львів - елемент множини міст України.

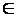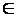      Якщо множину цифр десяткової нумерації по­значити через А, то належність числа цій множині можна позначити так: 5  А, 9  А.

      Число 12 не належить множині А, не є елемен­том цієї множини. Це твердження можна записати так: 12 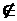 А.

      Множини бувають скінченні (множина будинків на певній вулиці) і нескінченні (множина точок пря­мої).

      Озн 2. Множина, у якій немає жодного еле­мента, називається порожньою. Позначається .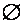

Наприклад, множина розв'язків рівняння 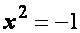  на множині дійсних чисел є порожньою, х  .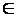

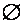      Множину можна задати:

      1. переліченням усіх її еле­ментів, наприклад {а, b, с} ;

      2. характеристичною властивістю, наприклад, В - множина чисел, крат­них 15, що менші від 90.

      Озн 3. Дві множини називаються рівними, якщо вони складаються з однакових елементів.

      Наприклад, X - множина коренів рівняння ;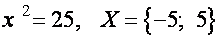

                         Y- множина коренів рівняння .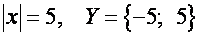

Х = Y.

      Озн 4. Якщо множина В складається з деяких елементів даної множини А і лише з них, то множина В називається підмножиною множини А.

Позначаємо це так: В 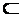 А.

     Наприклад, якщо В = {1, 2, 3}, А = {1, 2, 3, 4}, то В 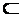 А.

     Множина В може складатися з усіх елементів множини А, тоді це можна записати так: В 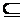 А.

    - знак строгого включення,

    - знак нестрогого включення.

Порожня множина є підмножиною будь-якої мно­жини.

Операції над множинами

      Над множинами можна виконувати певні опе­рації. Розглянемо три з них.

      Озн 5. Перетином множин А і В називається множина С, яка складається з усіх тих і лише тих елементів, які належать кожній із даних множин.

Позначаємо це так: А 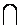 В = С .

 

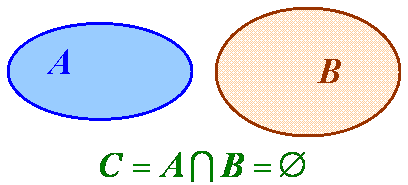
      Приклад 1.

      Нехай А - множина всіх дільників числа 32, В - множина всіх дільників числа 24. Отже,

      А = {1, 2, 4, 6, 8, 16, 32}, В= {1, 2, 3, 4, 6, 8, 12, 24}.

Тоді 

      С = А 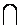 В, С = {1, 2, 4, 8}.

      Озн 6. Об'єднанням або сумою двох мно­жин А і В називається така множина R, яка скла­дається з усіх елементів множин А і В і лише з них.

Позначаємо це так:  .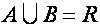

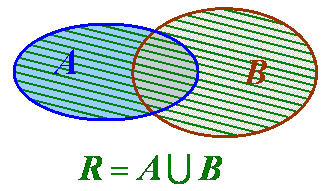
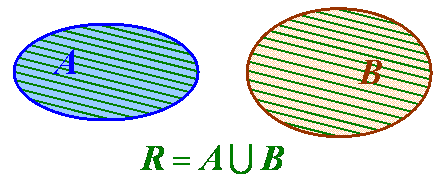
      Кожний зі спільних елементів береться в мно­жину R лише один раз.

Приклад 2.

      Для множин А і В з прикладу 1 об'єднанням буде

.

Приклад 3.

      Множина дійсних чисел є об'єднан­ням множин раціональних та ірраціональних чисел:

.

   

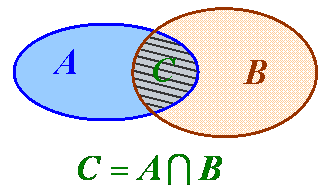
       Озн 7. Різницею двох множин А і В нази­вається така множина D, яка складається з усіх еле­ментів множини А, які не належать множині В.

Записуємо D = А\В.

Приклад 4.

А = {5, 6, 8, 12}, В = {5, 6}, D = А\В = {8, 12}.

Приклад 5.

А = {5, 6}, В = {5, 12, 6}, D = А\В = .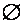

        Коли множина В є підмножиною множини A ( B 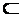 A ), то різниця D = А\В називається допов­ненням множини В відносно множини А і позна­чається .

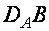Приклад 6.

А = {2, 4, 5}, В = {2, 4}, 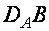 = {5}.

      Озн 8. Скінченна множина, для якої є істот­ним (важливим) порядок елементів, називається впорядкованою.

Вказати порядок розміщення елементів у скін­ченній множині з n елементів - означає поставити у відповідність кожному елементу даної множини певне натуральне число від 1 до n.

Приклад 7.

      Множини А = {1, 2, 7} і В = {2, 7, 1} є рівними, якщо вони невпорядковані, А = В.

Якщо ж вони є впорядкованими, то А 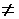 В.

Приклад 8.

      Із 30 учнів класу потрібно вибрати двох

      а) старосту і його заступника;

      б) для чергування у класі.

      У випадку а) - це впорядкована множина;

      у випадку б) - невпорядкована множина.